How To Find Slope With Only Y Intercept
In our Saturday guide to lines and angles, we dealt with parallel lines, perpendiculars, and the many different ways to observe angle measures with 2 or more lines. Now, nosotros'll wait at the other attribute of lines, namely their slopes and equations. This will be your complete guide to lines and slopes—what slopes mean, how to discover them, and how to solve the many types of slope and line equation questions yous'll encounter on the SAT. Earlier nosotros commencement, yous may want to take a moment to familiarize yourself with our guide to Sat coordinate points in order to refresh yourself on the nuts of coordinate geometry. Basically, coordinate geometry takes identify in the space where the $10$-axis and the $y$-axis meet. Any place on this infinite is given a coordinate point—written as $(ten, y)$—that indicates where the point is along each centrality. A line (or line segment) is a completely straight marker with no curvature. Information technology is made up of (and connects) a series of points together. A gradient is the measure of the slant (steepness) of a line. A gradient is found by finding the change in distance forth the y axis over the change in distance forth the $x$ axis. You lot are probably about familiar with this concept past finding the "rise over run" to observe the slope of a line. $${\change \in y}/{\alter \in 10}$$ Here is a typical line, presented on the coordinate grid. To discover our slope, first outset by marking the points where the line hits the grid at perfect integer coordinates. This will brand life simpler when we go to detect the slope. Wherever the grid meets at a corner, we will have coordinates that are integers. We can see here that our line hits the coordinates: $(-3, four)$, $(0, 2)$, and $(3, 0)$. At present let the states find the rise and run of the line. Our "rise" will exist -2, as we must move down 2 units to achieve the next coordinate point in our line. Our run will be +iii, equally we must motion 3 units to the correct to accomplish the side by side coordinate point in our line. So our final slope volition be: $\rise/\run$ $-{2/three}$ A slope can either exist positive or negative. A positive gradient rises from left to correct. A negative slope falls from left to right. A directly horizontal line has a slope of goose egg. It volition be defined by i axis only. $y=two$ A directly vertical line has an undefined slope (considering run will always exist 0, and you can't separate by 0). It will be divers past i axis simply. $ten=2.5$ The steeper the line, the larger the gradient. The red line is steepest, with a gradient of $iv/one$, or 4. The bluish line is not every bit steep, with a slope of $4/9$ San Francisco knows a little scrap most steep slopes. Finding the Slope $${y_2 - y_1}/{x_2 - x_1}$$ In guild to find the slope of a line that connects ii points, yous must notice the alter in the y-values over the change in the ten-values. (Annotation: It does not thing which points yous assign equally $(x_1,y_1)$ and $(x_2,y_2)$, so long as y'all are consistent.) Given the coordinates $(2, 2)$ and $(-1, 0)$, discover the slope of the line. Now, we can solve this question in one of two ways—past cartoon a graph and counting, or by using our formula. Since nosotros already saw earlier how it's possible to count out our slope on a graph, let u.s. use our formula to see how information technology's done. Of the 2 coordinate points, we must assign 1 set up to be $x_1$ and $y_1$ and the other to exist $x_2$ and $y_2$. Let united states pick (2, ii) to be our $x_1$ and $y_1$ and (-1, 0) to be our $x_2$ and $y_2$. ${y_2 - y_1}/{x_2 - x_1}$ $(0 - 2)/(-1 - 2)$ ${-2}/{-three}$ $two/3$ But what would accept happened had we assigned $(-1, 0)$ to be our $x_1$ and $y_1$ and $(ii, ii)$ to exist our $x_2$ and $y_2$? We would accept gotten the aforementioned results either style! ${y_2 - y_1}/{x_2 - x_1}$ $(2 - 0)/(2 - -ane)$ $2/3$ No matter which coordinates we assign to exist the offset or 2d values for ten and y, we will end up with the same slope then long as we are consistent. Equation of a Line $$y=mx+b$$ This is called the "equation of a line" or a line in "slope-intercept form" and information technology shows exactly how a line is positioned along the $10$- and $y$-axes besides every bit how steep it is. This is the nearly important formula yous'll need when it comes to lines and slopes, so allow'south suspension information technology into pieces. Find the equation of the line from the graph. We also determined earlier that the gradient is $ii/3$. Then when we put those ii pieces of information together, the equation of our line would exist: $y = {2/3}x + 0.five$ *If the question wants you to be more specific than "about a half" about what fraction of a number the line hits $10=0$ or $y=0$ at, it will accept a more detailed drawing. In this question, while the actual intercept for a line with coordinates $(2,ii)$ and $(0,-1)$ would actually be $2/3$ or $0.66$, not $0.5$, the graph is not at a calibration where yous could reasonably visually estimate that. Recollect to always re-write any line equations you are given into the proper course! Oft, the examination volition endeavor to trip you upwards by giving you an equation not written in proper form and asking for the gradient of the line. This is to get people to make a fault if they are going besides quickly through the exam. $$tx+12y=-three$$ The equation above is the equation of a line in the $xy$-plane, and $t$ is a constant. If the slope of the line is -x, what is the value of $t$? First, let u.s.a. put this equation into the proper equation of a line. $tx+12y = −3$ $12y = −tx−3$ $y = - {tx}/{12} -3/12$ At present, we only care about finding the slope, so let'southward find the value of t (our slope) past using our given. $-{t/12} = -x$ $-t = -120$ $t = 120$ Our last reply is $t = 120$. E'er remember to set upwards your equation as your first step and you'll be able to solve most whatsoever slope problem quickly and easily. When two lines come across at right angles, the lines are called "perpendicular." Perpendicular lines will always have slopes that are negative reciprocals of one another. This means that you must contrary both the sign of the slope as well as the fraction. For example, if a two lines are perpendicular to one another and one has a slope of $3/4$ the other line will accept a gradient of $-{iv/3}$. Perpendicular lines with slopes of $3/4$ and $-{4/3}$ And if a line has a slope of −5, the line that meets information technology perpendicularly will accept a gradient of $ane/5$. When two lines will never meet, no matter how infinitely long they extend, the lines are said to exist parallel. This means that they are continuously equidistant. If 2 lines are parallel, they volition also have the same slope. You can see why this makes sense, since the ascent over run will always have to be the aforementioned in order to make sure that the lines will never bear upon. Parallel lines with slopes of $4/3$ Most line and slope questions on the Sat are quite basic at their cadre. Yous'll generally run across ii questions on slopes per test and about all of them will only ask y'all to find the slope of a line or the equation of a line. The examination may attempt to complicate the question by using other shapes or figures, but the questions always boil down to these simple concepts. Just remember to re-write whatever given equations into the proper slope-intercept course and keep in mind your rules for finding slopes (and your rules for parallel or perpendicular lines). With this knowledge in mitt, you'll be able to solve these types of issues rapidly and hands. From the graph, we tin see that the y-intercept of the line is (0,one). The line likewise passes through the indicate (1,2). This is enough information for us to figure out the slope of the line, which we know is ${\alter \in y}/{\modify \in x}$. ${2-i}/{1-0}={1}/{ane}=1$ Now we know that the slope of the line is 1. In slope-intercept form, the equation for line $l$ is $y=10+1$ or choice D. Our final respond is D. We know that gradient is the ${\alter \in y}/{\change \in 10}$. The equation $y=kx +4$ is already in slope-intercept form, and so we know the gradient of the line is $k$. We also know that the line contains the point $(c,d)$ which means we tin substitute those variables for $(x,y)$ in the equation. This gives us $d=kc+4$ Solving for this equation for the slope, $grand$, gives usa $grand= {d-4}/c$ Our final answer is A, ${d-four}/c$ As you go through your line and gradient problems, continue in mind these tips: #one: Always rearrange your equation into $y=mx+b$ The examination makers will often nowadays you lot with an equation of a line that is not in proper grade, for case: $4y+3x=12$. If you are going too quickly through the test or if you forget to rearrange the given equation into proper slope-intercept course, y'all will misidentify the gradient of the line. And then always remember to rearrange your equation into proper form equally your first pace. $4y + 3x = 12$ => $y = −{iii/4}ten + 3$ #2: Always remember your $\ascension/\run$ It can be easy to make a mistake endeavour to observe the change in $x$ before finding the change in y, as our brains are used to doing things "in order." Keep conscientious runway of your variables in order to reduce careless mistakes of this nature. Remember the mantra of "rise over run" and this volition help yous always know to find your modify in y over your change in $x$. #3: Make your own graph and/or count to notice your slope Because the gradient is always "rise over run," you can always find the slope with a graph—whether from a given graph or from your own. It'southward never a bad idea to take a 2nd and make your own graph if you are not provided with one. This will assistance you better visualize the problem and avert errors. If you forget your formulas (or simply don't want to use them), simply count how the line rises (or falls) and trace its "run," and you will always find your slope. Now that nosotros've walked through the typical slope questions you'll see on the test (and a few bones tips you'll need to solve them), let's put your cognition to the exam. Answers: D, A, B, D Answer Explanations: 1. We know that slope is the ${\change \in y}/{\change \in x}$. Nosotros are also told that our slope is -2, which ways information technology must exist $-{2/1}$. This means that, for every time our y value decreases by ii, our x value increases by ane. And every time our y value increases by 2, our x value will decrease by 1. If we employ our rectangle, we too take i point of reference on the line. We can see that the rectangle has a length of 3 (because information technology spans horizontally from $x=0$ to $x=iii$) and a length of 4 (because information technology spans vertically from $y=0$ to $y=iv$). This ways that the rectangle hits the line at the top right corner at coordinates (3, 4). Now we can simply count where the line will hit the y-centrality. Because the gradient increases horizontally (along the x-axis) one unit at a time, we tin see that there will be $3/1 = 3$ even points forth the line needed to find the y-intercept. Basically, this means that nosotros are taking the slope, $-{ii/1}$, and multiplying it by 3 to get $-{half dozen/3}$. In other words, we are adding six to the alter in y and subtracting 3 from the alter in x because we are taking the slope backwards. So now we can discover our new point by maxim that we increased our y-value from 4 to $4+6=10$, and we have decreased our x-value from iii to $3−three=0$, which would give us the new slope of: $(iv + half dozen)/(3 - three) = 10/0$ So our new coordinate point is (0, 10), which means that our y-intercept is ten. Our final respond is D, 10. 2. We know that we tin can detect the slope of the line using ${y_2 - y_1}/{x_2 - x_1}$, so let's plug in our coordinates of (0,r) and (s,0) for these values. ${y_2 - y_1}/{x_2 - x_1}$ $(0 - r)/(s - 0)$ $r/s$ Our southward will remain unchanged, but our r value will go negative, as it is being subtracted from zero. Our last answer is A. 3. If you count to the point at which the line crosses the y-intercept, you can see it hits at $y=3$ In the equation $y=mx+b$, the b is the y-intercept. That means our b volition exist three. Nosotros can therefore cantankerous off answer choices A and D, leaving us downwardly to B, C, and Due east. We can also run across that our line falls from left to right, then our slope will be negative. This means we tin can eliminate answer selection Due east, leaving us between choices B and C. Now let's take the two points at which the line hits the axes. We already saw that the line hits the y-intercept at $y=3$ and nosotros tin can likewise see that the line hits the x-axis at $x=2$. This means our line hits coordinates (0, 3) and (2, 0). This means that the modify in our y value is -3 and the change in our x value is +2. (Why? Because we decreased our y value past iii and we increased our x value by two.) So our slope must be $-{3/2}$, which means that our last equation will be: $y = -{3/2}x + 3$ Our final answer is B. four. We're told that the equation of the line is $y=2x-5$. This means that the slope of the line is ii and the $y$-intercept is at (0,-five). A slope of ii means that, for each increase in $x$ of one, $y$ increases by ii. Looking at each of the graphs, choices C and D are the simply lines with a slope of two. (Don't be fooled by option B which has a slope of -2). Next nosotros tin can look at $y$-intercepts. The line in choice C has a $y$-intercept at ($0,5)$, which doesn't match the equation of the line we were given. However, option D's line has a $y$-intercept at $(0,-v)$, which is exactly what we're looking for. Option D is the only line with both the correct slope and y-intercept. Our terminal respond is D. Once you accept familiarized yourself with the basics of coordinate geometry, slopes should not be likewise far off field. Though the Sabbatum will try to complicate problems equally much equally they are reasonably able, questions on lines and slopes are virtually e'er easier than they appear. Go along your important formulas shut to your heart and be vigilant with your negative signs, and you'll exercise merely fine when it comes to slopes and intercepts. Phew! You've learned all in that location is to learn about your slopes angles. Luckily for you (for a sure definition of "luck"), in that location is so much more to learn! Before you keep on, make certain you accept a business firm grasp of all the topics covered on SAT math and so that you can see what to prioritize. If you're looking for a particular math topic, scope out our Sabbatum math annal for individual topic guides similar this ane. We've got guides to solid geometry, probability, ratios, and more! If you lot don't know where to begin, make sure you accept a exercise test and see how your score ranks. This will give you a good sense of where your strengths and weaknesses are and how you lot should focus your study time. Looking to get a perfect score? Cheque out our guide to getting an 800, written by a perfect scorer! Want to improve your Saturday score by 160 points? Check out our best-in-class online Sat prep plan. We guarantee your money dorsum if you don't amend your Sabbatum score by 160 points or more than. Our programme is entirely online, and it customizes what yous study to your strengths and weaknesses. If you liked this Math strategy guide, you lot'll beloved our program. Forth with more detailed lessons, you'll become thousands of practice issues organized by individual skills and then you lot learn most effectively. We'll also requite you a stride-by-step programme to follow so you'll never be confused about what to report adjacent. Check out our 5-day costless trial: 
What Are Lines and Slopes?



Backdrop of Slopes






Line and Slope Formulas

 We're using the same graph from above, and we can see that the line intersects with the $y$-axis at around $y=0.5.$*
We're using the same graph from above, and we can see that the line intersects with the $y$-axis at around $y=0.5.$*Perpendicular Lines

Parallel Lines

 When lines turn devious.
When lines turn devious. Typical Line and Slope Questions
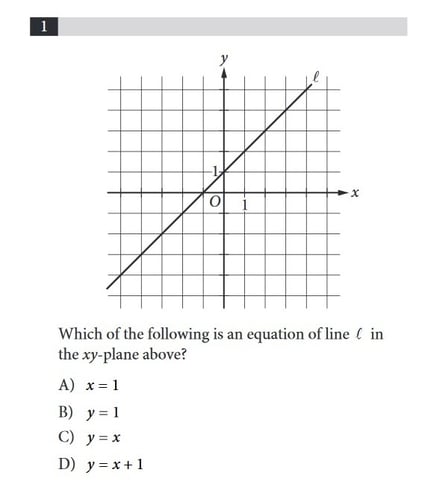

How to Solve a Line and Slope Problem
 Oh, for the days when all we needed to know well-nigh lines was how to colour in (or out of) them....
Oh, for the days when all we needed to know well-nigh lines was how to colour in (or out of) them.... Examination Your Knowledge
 Hurray, hurray! You've found your slopes, you know your lines! Congrats, congrats.
Hurray, hurray! You've found your slopes, you know your lines! Congrats, congrats. The Accept-Aways
What'southward Side by side?


About the Writer
Courtney scored in the 99th percentile on the SAT in loftier schoolhouse and went on to graduate from Stanford Academy with a caste in Cultural and Social Anthropology. She is passionate about bringing teaching and the tools to succeed to students from all backgrounds and walks of life, as she believes open pedagogy is one of the swell societal equalizers. She has years of tutoring experience and writes creative works in her free fourth dimension.
Source: https://blog.prepscholar.com/lines-slopes-sat-math-geometry-strategies-and-practice
Posted by: pettypubjewer.blogspot.com


0 Response to "How To Find Slope With Only Y Intercept"
Post a Comment